

Жизнь сама по себе штука непростая, но если наполнить её составными высказываниями, то она станет... проще!
Самое простое составное высказывание образуется с помощью отрицания не. Рецепт: берём высказывание и отрицаем его.
Например, простое высказывание СЕГОДНЯ ВЫХОДНОЙ превратится в составное высказывание СЕГОДНЯ НЕ ВЫХОДНОЙ.
Ещё один способ получить составное высказывание - объединить два простых высказывания связками и, либо или.
СЕГОДНЯ ВЫХОДНОЙ, У МЕНЯ ЕСТЬ ВЕЛОСИПЕД - простые высказывания. Соединив их союзом и получим сложное высказывание:
СЕГОДНЯ ВЫХОДНОЙ и У МЕНЯ ЕСТЬ ВЕЛОСИПЕД.
Таким образом и интуитивно понятно: когда выходной и при наличие велосипеда можно смело двигать в путь.
|
При этом к каждому простому высказыванию в связке с и, либо или можно отдельно применять отрицание. |
И вот что я вам хочу сказать:
if (СЕГОДНЯ ВЫХОДНОЙ и У МЕНЯ ЕСТЬ ВЕЛОСИПЕД):
Поехал кататься
Велосипед есть. Выходного нет. Сижу дома. Тем более за окном дождь льёт так, что не слышно шума машин на трассе. К тому же ночь. И это здорово!
|
|
ЛОГИЧЕСКИЕ СВЯЗКИ |
Всего их три. Перечислю логические связки в порядке приоритета. Что такое приоритет логических связок? В математике приоритетными (выполняемыми в первую очередь) считаются выражения в скобках. Далее следует умножение, деление, и в самом конце сложение и вычитание.
Например, (2 + 3) * (4 - 2 * 2) = 0. Правильно ли? Хорошо вы знаете арифметику? Проверьте с помощью Python, выполнив программу:
if ((2 + 3) * (4 - 2 * 2) == 0):
print("Правильно!")
else:
print("Неправильно!")
Существуют такие же правила для последовательности выполнения логических операций в сложных условиях. Речь, конечно же, идёт не о делении и отрицании, а о логических операциях (связках), вот они:
С помощью вышеприведённых логических связок образуются составные логические высказывания, и их общая истинность проверяется с помощью таблиц истинности.
|
|
ТАБЛИЦЫ ИСТИННОСТИ |
На самом деле таблицы истинности можно и не учить, если у вас хорошо развито логическое мышление. Проверьте себя.
Назовите целое число, которое не меньше 80 и не больше 150 и не меньше 90 или равно 150. Таких чисел может быть больше десятка. Найдите хотя бы одно.
Ответ
Во-вторых, число 150, т.к. указано "или равно 150"
В-третьих, подойдут все числа, которые больше 90 и меньше 150, например, 91, 92... 148, 149
То есть для правильного ответа подойдёт одно любое число из ряда: 90, 91, 92, 93, 94... и так далее, 148, 149, 150.
Если ответили правильно, то всё в порядке. Хорошее логическое мышление существенно облегчит вам программирование. Если возникли трудности, то придётся изучить таблицы истинности.
|
Составное логическое высказывание в таблице истинности может принимать лишь два значения: 1 или 0. Они символизируют True или False соответственно. Результатом также являются либо 1, либо 0. |
Проявите усердие и разберитесь с таблицами истинности. Поделюсь опытом - многим это кажется сложным. Придётся постараться. И тогда у вас всё получится!
|
|
ТАБЛИЦА ИСТИННОСТИ ДЛЯ NOT |
Для полноты картины возьмём выражение "Сегодня выходной". Выражение может быть либо истинным, либо ложным.
|
|
Таблица формируется следующим образом: берётся символ (вроде как переменная) и ему задаётся логическое выражение. Мы с вами знаем, что переменная может принимать любые допустимые типом переменных значения. То же и в случае с таблицами - мы рассматриваем любое логическое выражение и обозначаем его символом.
В нашем примере будет:
A = Сегодня выходной
Применение инверсии:
A = not A
Если воспроизвести на чистом русском языке, то высказывание "Сегодня выходной" превратится в "Сегодня не выходной". То есть станет обратным: если начальное - истина, то с добавлением "не" - ложь и наоборот.
В таблице выглядит так:
Обычно в первых, вертикальных, колонках таблицы указываются имена переменных. Имя может быть одно (как в случае с not) или два (в следующих таблицах). Под именем переменной подразумевается какое-либо простое логическое высказывание. Например, A = "СЕГОДНЯ ВЫХОДНОЙ" или B = "УЧЕНЬЕ - СВЕТ".
Так как у нас операция not, то требуется лишь одно высказывание. Обозначим его переменной A. И к высказыванию применим операцию not.
Оформление таблицы на русском языке, без вот этих вот математик и переменных:
Надеюсь, информация поможет с лёгкостью понять следующие таблицы истинности. Их будет всего две.
|
|
ТАБЛИЦА ИСТИННОСТИ ДЛЯ AND |
Логическая связка and, оно же "и", оно же конъюнкция, допустима для связки двух простых логических выражений.
|
|
Примем за A первое логическое высказывание:
A = "Москва является столицей России".
За B - второе высказывание:
B = "Луна является спутником Земли".
Тогда выражение А и B будет истинным. Попробуйте сами. Я задам вопрос и потребую, чтобы вы ответили только "да" или "нет":
- Москва является столицей России и Луна является спутником Земли?
Как вы ответите?
А на этот вопрос:
- Москва является столицей России и планета Земля плоская?
Итак, у нас новенькое:
A = Москва является столицей России
B = Планета Земля плоская
Тогда результат составного логического выражения A и B равен False, так как A - Истина, а B - Ложь (Надеюсь, что наше высказывание B, содержащее утверждение, что "Планета Земля плоская", является ложью. Так, по крайней мере, привычней. А Максу Ожерельеву привет!)
Таблица истинности для and:
Последняя строка: истинным выражение A и B становится только в том случае, когда и A, и B являются истинными.
Не напоминает ли результат умножения 0 х 0 = 0, 0 х 1 = 0, 1 х 0 = 0, 1 х 1 = 1? Поэтому конъюнкцию и называют - логическое умножение. Так будет проще запомнить.
|
|
ТАБЛИЦА ИСТИННОСТИ ДЛЯ OR |
Логическая связка or, оно же "или", оно же дизъюнкция, допустима для связки двух простых логических выражений.
|
|
Таблица истинности для or:
Дизъюнкцию ещё называют логическим сложением. Посмотрите на таблицу истинности: в последнем столбце всегда результат сложения. Последнюю строку (1 + 1 = 1) будем считать исключением.
|
|
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ |
Составные высказывания позволяют осуществлять проверку нескольких связанных параметров программы единовременно. Высказывания могут использоваться как в условиях, так и являться отдельными выражениями, результат которых может быть присвоен переменной.
Нам требуется проверить, входит ли находящееся в переменной day число в диапазон от 1 до 7 включительно. Две представленные программы равнозначны:
day = 3
if (day >= 1 and day <= 7):
print("Число входит в диапазон")
Здесь мы проверяем выражение (day >= 1 and day <= 7) непосредственно в условии. Так можно. И многие программисты так и поступают.
В данном случае всё выражение будет истинным только тогда, когда переменная day содержит больше или равное единице число и (в то же время) меньше или равное семи.
Вспомним таблицу истинности для and: только при наличии 1 и 1 результатом будет истина. Также и здесь: два простых выражения day >= 1, day <= 7 должны быть истинными одновременно.
Вторая программа. Смысл её полностью повторяет смысл предыдущей:
day = 3
res = (day >= 1 and day <= 7)
if (res):
print("Число входит в диапазон")
В этой программе мы не сразу проверяем выражение на истинность. Строка res = (day >= 1 and day <= 7) означает, что в переменную res поместится результат составного высказывания (day >= 1 and day <= 7). И только потом if проверит значение res. В случае, когда res истинно, условие "сработает" и выведет на экран надпись "Число входит в диапазон".
Наберите программу (желательно разберитесь со второй). Изменяйте значение переменной day до тех пор, пока не поймёте всё и полностью.
|
Ещё можно записать так: (day >= 1) and (day <= 7). Разницы с точки зрения логики никакой. Есть разница только с точки зрения восприятия текста человеком. |
Сложные условия, выраженные с помощью логических связок not, and, or, существенно облегчают контроль значений, проверку разнообразных условий, делая код простым и понятным. Только нужно разобраться, как и обычно.
|
|
НАЗОВИТЕ ЧИСЛО |
Составим программу, решающую нашу предыдущую задачу.
Назовите число, которое не меньше 80 и не больше 150 и не меньше 90 или равно 150. Таких чисел может быть больше десятка. Найдите хотя бы одно.
Решение:
print("""Назовите число, которое
не меньше 80 и не больше 150 и
не меньше 90 или равно 150.
Таких чисел может быть
больше десятка. Найдите
хотя бы одно.""")
x = int(input("Введите предполагаемое число: "))
# Обратите внимание на знак \ в конце следующей строки кода.
# Это оператор переноса в Python - тождественен
# литературному пере-
# носу слов. С помощью \ можно дробить строки
# на части, если они длинные.
# Знак # означает комментарий. Всё, что записано
# после него - выполняться не будет. Можете не набирать
# строки с комментариями
res = (not(x < 80) and not(x > 150) \
and not(x < 90) or (x == 150))
if (res):
print("Вы угадали!")
else:
print("К сожалению, не то...")
input("Нажмите ENTER для выхода...")
quit()
О! В тексте что-то новенькое! Изучаем
1. Тройные парные кавычки функции print() означают, что текст будет многострочный. Используя """ перед текстом и """ после текста будьте уверены - Python выведет текст на экран в ровном соответствии с расположением текста в теле программы. Все переносы сделает. Удобно для вывода многострочного текста, например, для инструкций.
Только не забывайте "закрыть" текст также тремя кавычками, идущими подряд.
print("""Этот
текст
будет
выведен
в пять строк""")
2. "Пустая" функция input() на предпоследней строке. Она нужна для того, чтобы спровоцировать задержку программы. Чуть ниже об этом.
3. quit(). Выход из интерпретатора. Когда Shell дойдёт до выполнения этой команды, то услужливо спросит:
Смело нажимайте ОК - Python закроет окно Python Shell, но откроет его при следующем запуске.
|
|
ЗАПУСКАЕМ ПРОГРАММУ В WINDOWS |
Найдите файл с вашей программой в обычном проводнике Windows. Не нужно его загружать в Python, просто дважды щёлкните на нём мышью.
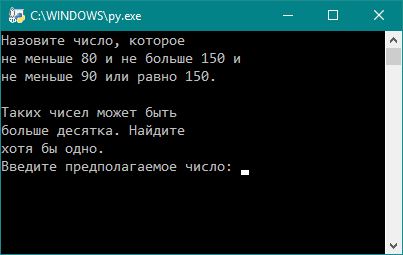
Если вы установили язык программирования в точности с инструкциями главы "Python", то программа запустится и вы можете так же вводить значения и наблюдать результат работы, как и в Python Shell.
Откройте файл с программой простым текстовым редактором, например, Блокнотом (рекомендую Notepad++), и удалите предпоследнюю строку: input("Нажмите ENTER для выхода...").
Вновь запустите программу двойным кликом мыши из проводника Windows. Введите число... и? Что случилось?
Для тех, кто не сделал
Это происходит потому, что после выполнения последней команды консольное окно с результатами сразу закрывается.
Получается, что input("Нажмите ENTER для выхода...") приостанавливает выполнение программы, ожидая ввода значения или просто нажатия Enter.
При этом результат ввода, то есть та строка, которую мы имеем возможность набрать, никуда не попадает, она "не запоминается" компьютером, так как результат функции input("Нажмите ENTER для выхода...") не поступает ни в какую переменную, то есть слева мы не записали имя переменной, например, s = input("Нажмите ENTER для выхода...")
|
|
СЕГОДНЯ ВЫХОДНОЙ? |
Узнали? Согласны?
day = int(input("Введите номер дня недели: "))
if (day == 7):
print("Сегодня выходной. Едем кататься на велосипеде.")
elif (day < 1):
print("Такого дня не существует.")
elif (day > 7):
print("Такого дня не существует.")
else:
print("Сегодня будний день.")
Перепишем программу с использованием сложных условий:
day = int(input("Введите номер дня недели: "))
if (day < 1 or day > 7):
print("Такого дня не существует.")
elif (day == 7):
print("Сегодня выходной. Едем кататься на велосипеде.")
else:
print("Сегодня будний день.")
Код стал короче. А краткость, как известно, сестра таланта.
|
|
НАРУШАЕТ ЛИ ВОДИТЕЛЬ? |
Ещё одна программа, которую мы можем переделать с полным правом:
speed = int(input("Введите скорость автомобиля: "))
if (speed > 200):
print("Это не самолёт. Такой скорости не существует.")
elif (speed > 60):
print("Водитель нарушает! Штраф ему, штраф!")
elif (speed == 0):
print("Автомобиль стоит на месте.")
elif (speed < 0):
print("Отрицательной скорости не существует.")
else:
print("Водитель не нарушает.")
Попробуйте сделать самостоятельно. Сократите программу с помощью использования сложных условий.
speed = int(input("Введите скорость автомобиля: "))
if (speed > 60 and speed <= 200):
print("Водитель нарушает! Штраф ему, штраф!")
elif (speed > 200):
print("Это не самолёт. Такой скорости не существует.")
elif (speed == 0):
print("Автомобиль стоит на месте.")
elif (speed < 0):
print("Отрицательной скорости не существует.")
else:
print("Водитель не нарушает.")Ответ
![]()
Но я всё же добавил сложное условие :)
Пожалуй, на этом со сложными условиями пора кончать. Вы ещё встретитесь с ними на просторах программирования, а нам пора идти дальше. Впереди много забавного!
|
© 2019-2024 Виктор Трофимов
|